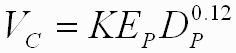
and K is a proportionality constant.
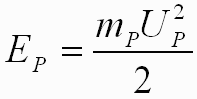
and Up is the velocity of the micrometeoroid in km/sec,
and mp is the mass of the projectile in grams.
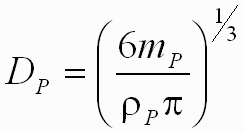
and
Pamela Generie - formerly of the Goddard Space Flight Center
October 27, 1995
The MOLA II micrometeoroid environment is more severe than the MOLA I micrometeoroid environment. Therefore, an analysis was done to determine the percent of surface area of the Primary Mirror that may be damaged due to micrometeoroids for MOLA II. A conservative analysis determined that only 0.002% of the Primary Mirror surface, which is equivalent to 0.030 cm2, may be damaged due to micrometeoroids.
The analysis can be broken into 3 steps:
The classical method for calculating a crater size is to use the equation taken from Chapter 6 "Hypervelocity Impact Mechanics" by Al Swift. The average velocity of a micrometeoroid is 20 km/sec and the average density of a micrometeoroid is 2.5 grams/cm3.
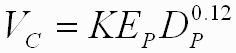 | where Vc is the volume of the crater, and K is a proportionality constant. | |
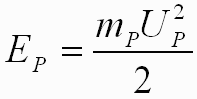 | where Ep is the Kinetic Energy of the Projectile,
and Up is the velocity of the micrometeoroid in km/sec, and mp is the mass of the projectile in grams. |
|
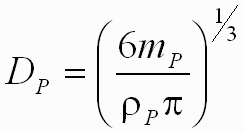 | where Dp is the projectile diameter,
and |
The proportionality constant K is frequently determined through hypervelocity impact testing. However, due to the hazardous nature of beryllium dust particles, there are few publications documenting hypervelocity impact testing on beryllium. Since the materials behave similar to fluids in a hypervelocity impact, an approximation of K is to take the square root of the ratio of the micrometeoroid and mirror densities.
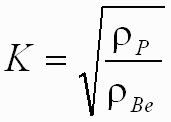
Another approximation for K, as suggested by Al Swift, is to use the K value for fused silica since beryllium behaves similar to fused silica under a hypervelocity impact. Both approximations result in nearly equivalent K values.
The projectile is assumed to be spherical. The resulting crater will be hemispherical. Once Vc, volume of the crater, is determined, then the diameter of the crater, Dc, may be easily determined.
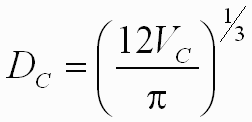
Using the above equations, it is possible to estimate the Primary Mirror surface area that will be damaged due to a micrometeoroid of a given mass.
| Mass of Micrometeoroid (grams) | Crater Diameter (cm) | Damaged Primary Mirror Surface Area (cm2) |
|---|---|---|
| 3.16E-06 | 0.119 | 0.011 |
| 1.00E-05 | 0.177 | 0.025 |
| 3.16E-05 | 0.264 | 0.055 |
| 1.00E-04 | 0.394 | 0.122 |
| 3.16E-04 | 0.586 | 0.270 |
The expected number of impacts is a function of the total mission fluence (F), the flight path, and the exposed surface area (A) of the Primary Mirror.
Expected Number of Impacts = A F
The parabolic surface area of the Primary Mirror is 0.196 m2. However, according to Rene Ageuro (Mars Global Surveyor micrometeoroid analyst at JPL), the value that should be used for the Primary Mirror surface area is 0.128 m2. This value takes into account the flight path and the solid angle of the mirror that is exposed to micrometeoroids.
The total mission fluence varies with the mass of the micrometeoroids. This analysis is conservative because the values used for the total mission fluence are high, according to Rene Aguero. This is because the fluence values presented here are omnidirectional. The total mission fluence values for MOLA II are only a fraction (10%) of the omnidirectional total mission fluence values.
The probability of at least one impact of a micrometeoroid of a given size on the Primary Mirror is given in Table 2. The equation used to calculate the probability is:
Probability of at least one impact = 1 - P(no impacts) = 1 - e -AF
| Mass of Micrometeoroid (grams) |
Total Mission Fluence (F/m2) |
Expected # of Impacts on Primary Mirror |
Probability of at Least One Impact |
|---|---|---|---|
| 3.16E-06 | 5.96E+00 | 7.63E-01 | 0.53 |
| 1.00E-05 | 2.55E+00 | 3.26E-01 | 0.28 |
| 3.16E-05 | 9.64E-01 | 1.23E-01 | 0.12 |
| 1.00E-04 | 4.04E-01 | 5.17E-02 | 0.05 |
| 3.16E-04 | 1.16E-01 | 1.48E-02 | 0.01 |
Using the information in Tables 1 and 2, the graph of the expected number of impacts of a micrometeoroid of a given mass and the surface area damaged per impact can be integrated to obtain the total Primary Mirror surface area damaged.
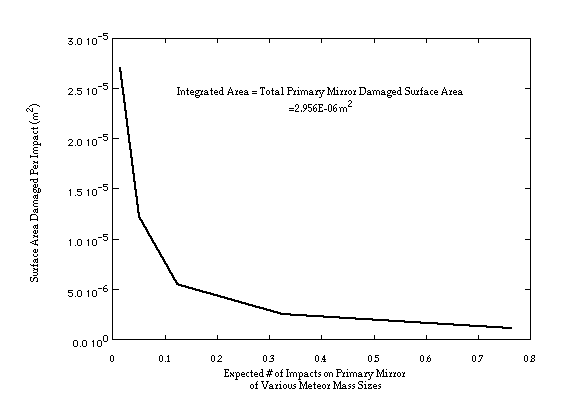
The conservative estimate of damaged Primary Mirror surface area is 0.030 cm2. This is approximately 0.002% of the total parabolic Primary Mirror surface area.
Rene Aguero provided me with additional information which allowed me to conduct a more detailed analysis than the one presented here. The information he provided included different velocities for various micrometeoroid mass sizes and fluence values specific to the MOLA II Primary Mirror. The more detailed analysis estimated the damaged Primary Mirror surface area to be 0.00026 cm2.